6 – Wikipedia

Nombre naturel

Nombre naturel

6 (six) est le nombre naturel suivant 5 et le 7 précédent. C'est un nombre composite et le plus petit nombre parfait.^[1]

En mathématiques

Un polygone à six côtés est un hexagone,^[1] L'un des trois polygones réguliers capables de carreler l'avion. Un hexagone a également 6 bords ainsi que 6 angles internes et externes.

6 est le deuxième plus petit numéro composite.^[1] C'est également le premier numéro qui est la somme de ses diviseurs appropriés, ce qui en fait le plus petit nombre parfait.^[2] C'est également le seul numéro parfait qui n'a pas de racine numérique de 1.^[3] 6 est le premier nombre parfait unitaire, car c'est la somme de ses diviseurs unitaires propres positifs, sans inclure. Seuls cinq de ces nombres sont connus pour exister.^[4] 6 est le plus grand des quatre nombres All-Harshad.^[5]

6 est le 2e numéro composite supérieur supérieur,^[6] le 2e nombre colossalement abondant,^[7] le 3ème numéro triangulaire,^[8] le 4e numéro hautement composite,^[9] un numéro proronique,^[10] un numéro congruent,^[11] un numéro de diviseur harmonique,^[12] et une semi-7.^[13] 6 est également le premier numéro de Granville, ou ${\ displayStyle {\ Mathcal {s}}}$-NIGRAGE PERFECT. Un souverain de Golomb de la longueur 6 est un « souverain parfait ».^[14]

Le théorème des six exponentiels garantit que dans certaines conditions, l'un des six exponentiels est transcendantal.^[15] Le plus petit groupe non abélien est le groupe symétrique ${\ displayStyle \ Mathrm {S_ graveur laser bois}}$ graveur laser bois}} »/> qui a 3! = 6 éléments.^[1] 6 La réponse au problème du numéro de baisers bidimensionnel.^[16]

Un cube a 6 faces. Un tétraèdre a 6 bords. En quatre dimensions, il existe un total de six polytopes réguliers convexes.

Dans la classification des groupes simples finis, vingt des vingt-six groupes sporadiques de la famille heureuse font partie de trois familles de groupes qui divisent l'ordre du géant amical, le plus grand groupe sporadique: cinq première génération Groupes Mathieu, sept deuxième génération sous-quotents du treillis de sangsue et huit troisième génération Sous-groupes du géant amical. Le reste six Les groupes sporadiques ne divisent pas l'ordre du géant amical, qui sont appelés parias (Ly, SUR, Ru, J₄, J₃et J₁).^[17]

6 est le plus petit entier qui n'est pas un exposant d'un nombre premier, ce qui en fait le plus petit entier supérieur à 1 pour lequel il n'existe pas de champ fini de cette taille.^[18]

Liste des calculs de base

Division	1	2	3	4	5	6	7	8	9	10		11	12	13	14	15
6 ÷ x	6	3	2	1.5	1.2	1	0.857142	0,75	0.6	0.6		0.54	0,5	0.461538	0.428571	0.4
x ÷ 6	0.16	0.3	0,5	0.6	0.83	1	1.16	1 et 13	1.5	1 et 16		1.83	2	2.16	23	2.5

Exponentiation	1	2	3	4	5	6	7	8	9	10		11	12	13
6x	6	36	216	1296	7776	46656	279936	1679616	10077696	60466176		362797056	2176782336	13060694016
x6	1	64	729	4096	15625	46656	117649	262144	531441	1000000		1771561	2985984	4826809

Parties de mots grecs et latins

Hexa

Hexa est le grec classique pour « six ».^[1] Ainsi:

Le préfixe sexe-

Sexe- est un préfixe latin signifiant « six ».^[1] Ainsi:

• Senary L'adjectif ordinal signifie-t-il « sixième »^[22]
• Les personnes atteintes de sexdactyment ont six doigts de chaque main
• L'instrument de mesure appelé Sextant a obtenu son nom car sa forme se forme un sixième d'un cercle entier
• Un groupe de six musiciens s'appelle un sextuor
• Six bébés livrés dans une naissance sont les sextuplets
• Paires de choix sexy – les paires de choix différaient par six sont sexyparce que le sexe est le mot latin pour six.^[23][24]

Le préfixe SI pour 1000⁶ est exa- (e), et pour son atto- (a) réciproque.

Évolution du chiffre hindou-arabique

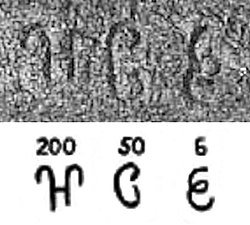
L'évolution du chiffre moderne 6 semble être plus simple par rapport aux autres chiffres. Le 6 moderne peut être retracé aux chiffres brahmi de l'Inde, qui sont d'abord connus des édits d'Ashoka c.250 BCE.^{[25][26][27][28]} Il a été écrit en un coup comme une minuscule cursive E tournée à 90 degrés dans le sens des aiguilles d'une montre. Progressivement, la partie supérieure de la course (au-dessus du glissement central) est devenue plus courbe, tandis que la partie inférieure de l'AVC (sous le glissement central) est devenue plus droite. Les Arabes ont laissé tomber la partie de la course sous le gribouillage. De là, l'évolution européenne vers notre 6 moderne était très simple, à part un flirt avec un glyphe qui ressemblait plus à un G. majuscule G.^[29]

Sur les affichages à sept segments de calculatrices et de montres, 6 est généralement écrit avec six segments. Certains modèles de calculatoires historiques n'utilisent que cinq segments pour le 6, en omettant la barre horizontale supérieure. Cette variante des glyphes n'a pas fait son chemin; Pour les calculatrices qui peuvent afficher des résultats en hexadécimal, un 6 qui ressemble à un « B » n'est pas pratique.

Tout comme dans la plupart des polices de caractères modernes, dans les polices de caractères avec des figures de texte, le caractère du chiffre 6 a généralement un ascension, comme, par exemple, dans .^[30]

Ce chiffre ressemble à un inversé 9. Pour désambigurer les deux sur des objets et des documents qui peuvent être inversés, le 6 a souvent été souligné, à la fois dans l'écriture manuscrite et sur les étiquettes imprimées.

Chimie

Anthropologie

bouddhisme

Le bouddhisme décrit six domaines de l'existence ou des domaines dans lesquels les êtres peuvent renaître en fonction de leurs actes. Ils sont visualisés sur la roue tibétaine de la vie et illustrent l'existence cyclique perpétuelle en samsara. Les six perfections ou «six paramitas» sont parmi les symboles bouddhistes les plus connus des six. Dans le bouddhisme mahayana, ce sont des qualités spirituelles fondamentales sur le chemin du bodhisattva pour atteindre le nirvana.

Voir aussi

Références

Liens externes